El movimiento que hay que volver atrás es el enroque largo, con lo que la posición de inicio quedaría así: 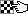. Era de esperar, en vista de mi primera pista, aunque no es evidente en absoluto por qué precisamente este "desmovimiento" es el bueno. De hecho, la primera impresión es que da exactamente igual lo que haga el blanco, porque el negro se enroca y no hay mate a corto (o ni siquiera a medio) plazo. A no ser, claro, que el enroque negro sea ilegal.

Veamos. De acuerdo con las leyes del ajedrez, si el blanco ha podido enrocarse (es la jugada que acabamos de deshacer) es porque hasta ese momento su rey no se había movido de e1. Ahora bien, en tal caso ¿cómo diantres ha viajado la torre de h1 hasta e3? Descartada la telequinesia, y haciendo nuestra la frase de Sherlock Holmes, la única respuesta posible, por improbable que parezca, ha de ser la correcta: la torre de d3 no es la de h1, que ha tenido que desaparecer del tablero tras ser capturada en su casilla inicial (o en g1 o f1) por una pieza negra, digamos un caballo. ¿Cómo se justifica entonces la presencia de una torre blanca en d3? No cabe más que una explicación: ¡es el resultado de coronar un peón! Si contáis, veréis que quedan siete peones blancos en el tablero; falta uno, justo el que ha promocionado a torre.

La siguiente pregunta es: ¿en qué casilla ha coronado el peón? Dando por sentado que el bando negro conserva su derecho a enrocar, es claro que no puede ser una de las del ala de dama, porque entonces la torre recién nacida, para llegar a d3, tendría que haber pasado a la fuerza por d8, dando jaque y obligando al rey negro a moverse de e8. Las casillas f8 y e8 se descartan por razones semejantes, y h8 también es ilícita porque es obligatorio que la torre haya estado siempre ahí para que el enroque sea posible.

Esto nos deja g8 como última opción. No parece muy verosímil, pero nada en este problema lo es, y teóricamente es factible, con una pieza en f8 haciendo de escudo y la nueva torre escapando por la columna g. Pero escarbemos un poco más: ¿qué peón blanco, exactamente, es el que ha coronado en g8? El situado al inicio de la partida en a2 seguro que no, ya que solo podría haber llegado a g8 capturando en diagonal y ello le habría obligado a pasar por f7. A la vista de cómo se distribuyen el resto de peones, no caben más que dos alternativas: o ha sido el de b2, o el de e2. Caso de ser el de b2, habría tenido que capturar cinco veces para llegar a g8, lo que implica que el de f6 es el que empezó en e2, y el de b4 el que empezó en a2. Ello exige un par de capturas más, hasta un total de siete. Si fue el peón de e2 el que coronó también se requieren siete capturas, a saber: dos para viajar de la columna e a la columna g, cuatro para que el peón de b2 se traslade a f6, y la última de nuevo para ir de a2 a b4.

Siete capturas, pues (como mínimo), en cualquier caso. Pero echad cuentas: quedan diez piezas negras en el tablero, así que solo han podido desaparecer seis. La conclusión, reductio ad absurdum, es que el blanco no ha coronado en g8, ergo ha coronado en cualquier otro sitio, ergo el negro ha perdido su derecho a enrocar.

Y así llegamos al fantástico epílogo del problema. Una vez descartada 1...O-O como posible respuesta, el plan de las blancas está claro: abrir la columna, doblar torres y dar mate en d8. En concreto, 1.dxc3 parece decisiva, ya que 1...Kf8 permite 2.Rd8#. Sin embargo 1...gxf2+! obliga a perder un tiempo, 2.Kxf2, y como el blanco precisa dos jugadas más (Rad1 y Rd8) no hay mate en 3. ¿Vislumbráis ya la solución? El blanco, tras "arrepentirse" de su jugada inicial, se lo piensa mejor y mueve otra vez 1.O-O-O! 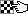. Ahora sí es mate en 3:

1...gxf2 El matiz es que tras el enroque esto no es jaque. Si 1...Kf8 entonces 2.Rd8#, como ya se ha explicado. Tampoco vale 1...cxd2+ 2.R1xd2 gxf2 3.Rd8#. 2.dxc3 f1=Q 3.Rd8# ¡Elemental, querido Watson! 1-0 [Comentarios parcialmente basados en notas de Hochberg]